Essay: Where Can Quantum Geometry Lead Us?

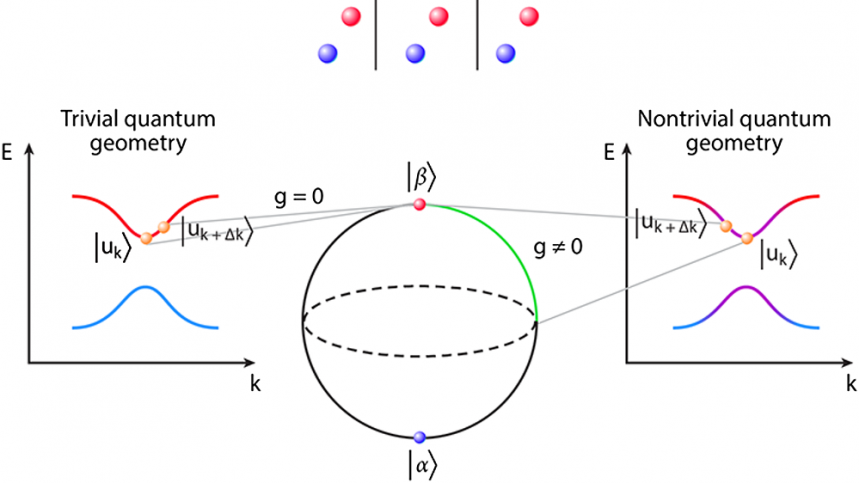
Quantum geometry defines the phase and amplitude distances between quantum states. The phase distance is characterized by the Berry curvature and thus relates to topological phenomena. The significance of the full quantum geometry, including the amplitude distance characterized by the quantum metric, has started to receive attention in the last few years. Various quantum transport and interaction phenomena have been found to be critically influenced by quantum geometry. For example, quantum geometry allows counterintuitive flow of supercurrent in a flat band where single electrons are immobile. In this Essay, I will discuss my view of the important open problems and future applications of this research topic and will try to inspire the reader to come up with further ideas. At its best, quantum geometry can open a new chapter in band theory and lead to breakthroughs as transformative as room-temperature superconductivity. However, first, more experiments directly showing the effect of quantum geometry are needed. We also have to integrate quantum geometry analysis in our most advanced numerical methods. Further, the ramifications of quantum geometry should be studied in a wider range, including electric and electromagnetic responses and interaction phenomena in free- and correlated-electron materials, bosonic systems, optics, and other fields.

Part of a series of Essays which concisely present author visions for the future of their field.

Read the whole essay in PRL.