Flat band Josephson junctions with quantum metric

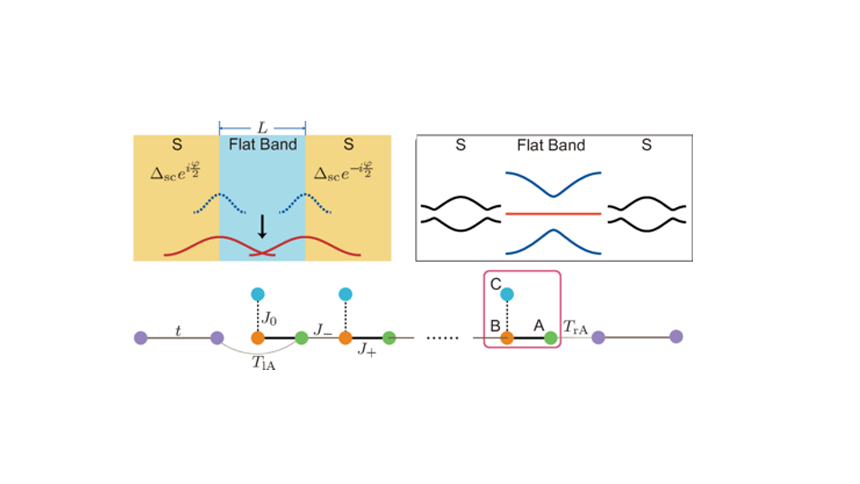
In this work, we consider superconductor/flat band material/superconductor (S/FB/S) Josephs on junctions (JJs) where the flat band material possesses isolated flat bands with exactly zero Fermi velocity. Contrary to conventional S/N/S JJs where the critical Josephson current vanishes when the Fermi velocity goes to zero, we show in this work that the critical current in the S/FB/S junction is controlled by the quantum metric length 𝜉QM of the flat bands. Microscopically, when 𝜉QM of the flat band is long enough, the interface bound states originally localized at the two S/FB, FB/S interfaces can penetrate deeply into the flat band material and hybridize to form Andreev bound states (ABSs). These ABSs are able to carry long range and sizable supercurrents. Importantly, 𝜉QM also controls how far the proximity effect can penetrate into the flat band material. This stands in sharp contrast to the de Gennes’ theory for S/N junctions which predicts that the proximity effect is expected to be zero when the Fermi velocity of the normal metal is zero. We further suggest that the S/FB/S junctions would give rise to a new type of resonant Josephson transistor which can carry a sizable and highly gate-tunable supercurrent.

Read the whole article by Li et al. in Physical Review Research