Fractional quantization in insulators from Hall to Chern

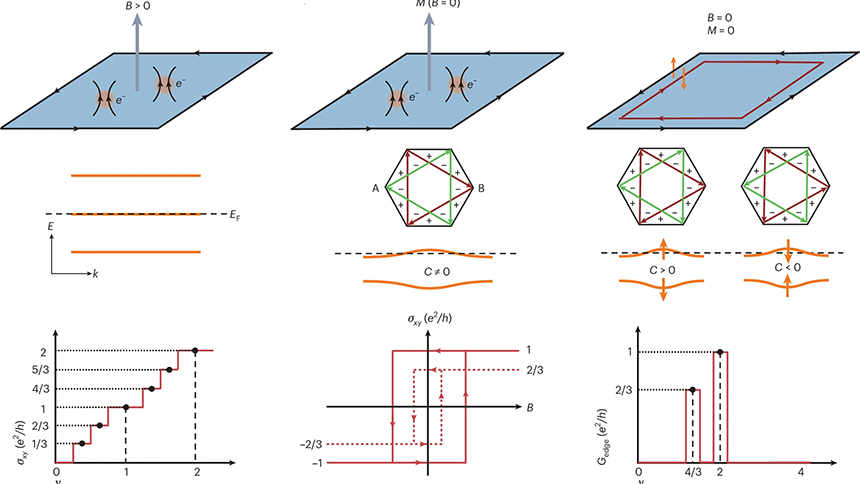
The discovery of the integer and fractional quantum Hall effects naturally prompted the question of whether these effects can be realized without a magnetic field. Answering this is fundamentally important and requires a synthesis of the concepts of band topology, quantum geometry and electronic correlations. Here we summarize the basic concepts of both fractional Chern and fractional topological insulators and illustrate them with the theoretical lattice models that support the flat Chern bands in which the states were first predicted. We then examine their experimental realizations in twisted bilayer transition metal dichalcogenides and moiré rhombohedral few-layer graphene. We also discuss the future challenges and opportunities in this research field.

Read the whole article by Bernevig et al. in Nature Physics.