“Quantum Geometric Nesting” and Solvable Model Flat-Band Systems

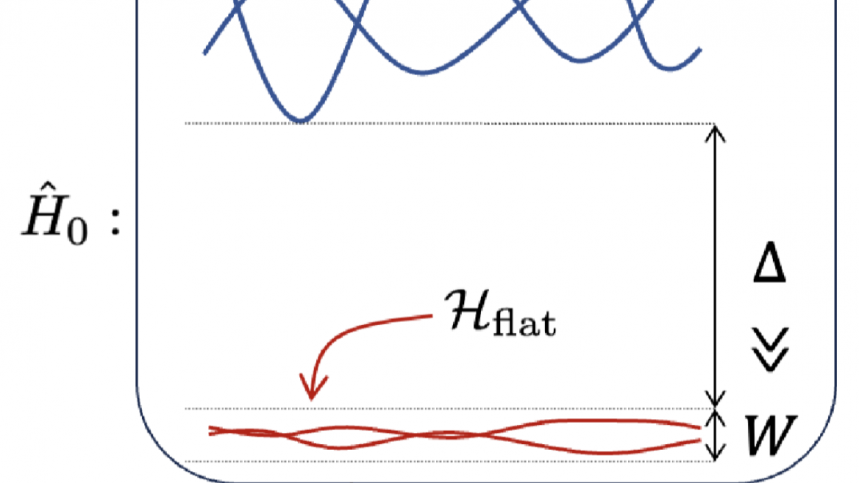
We introduce the concept of “quantum geometric nesting” (QGN) to characterize the idealized ordering tendencies of certain flat-band systems implicit in the geometric structure of the flat-band subspace. Perfect QGN implies the existence of an infinite class of local interactions that can be explicitly constructed and give rise to solvable ground states with various forms of possible fermion bi-linear order, including flavor ferromagnetism, density waves, and superconductivity. For the ideal Hamiltonians constructed in this way, we show that certain aspects of the low-energy spectrum can also be exactly computed including, in the superconducting case, the phase stiffness. Examples of perfect QGN include flat bands with certain symmetries (e.g. chiral or time-reversal), and non-symmetry-related cases exemplified with an engineered model for pair-density-wave. Extending this approach, we obtain exact superconducting ground states with nontrivial pairing symmetry.

Read more on arXiv.