Quantum Geometry of Time-Reversal Symmetry Breaking in Flat-Band Superconductivity

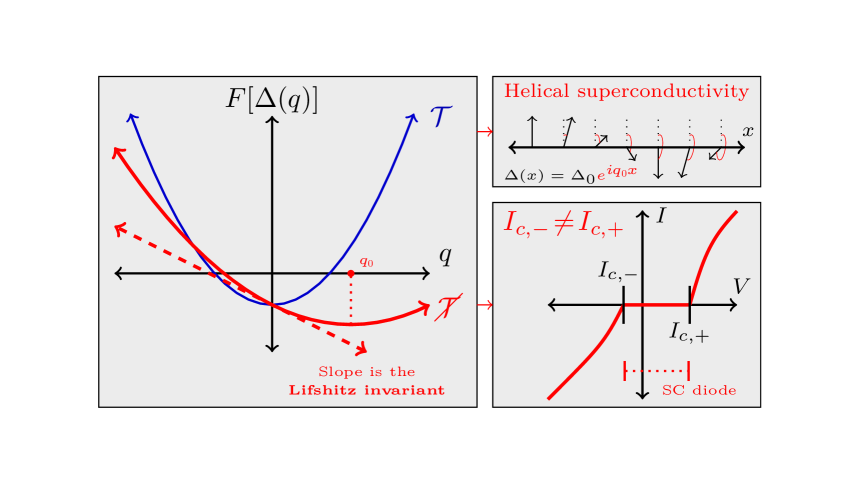
Several physical phenomena in superconductors, such as helical superconductivity and the diode effect, rely on breaking time-reversal symmetry. This symmetry-breaking is usually accounted for via the Lifshitz invariant, a contribution to the free energy which is linear in the phase gradient of the order parameter. In dispersive single-band superconductors with conventional pairing, the Lifshitz invariant can be computed from the asymmetries of the spectrum near the Fermi surface. We show that in multi-band superconductors, the quantum geometry also contributes to the Lifshitz invariant, and this is the dominant contribution when the low-energy bands are flat.

Read the whole article by Dunbrack et al. on arXiv.