Variational Diagrammatic Monte Carlo Built on Dynamical Mean-Field Theory

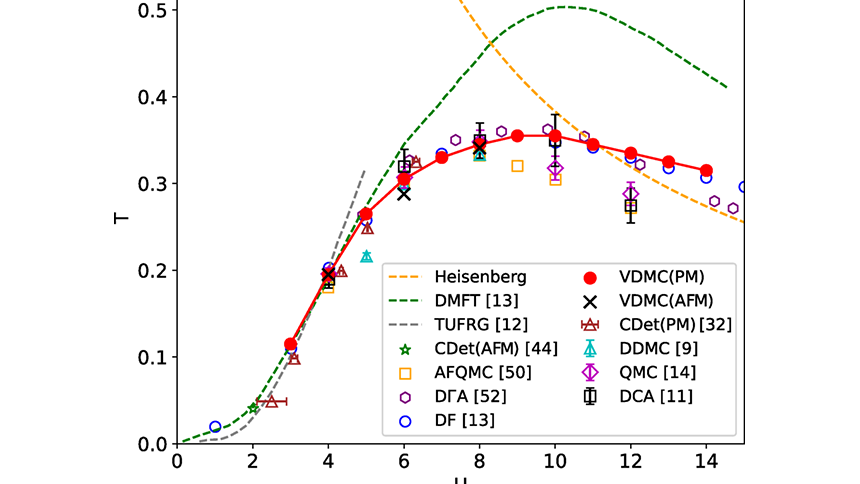
We develop a variational perturbation expansion around dynamical mean-field theory (DMFT) that systematically incorporates nonlocal correlations beyond the local correlations treated by DMFT. We apply this approach to investigate how the DMFT critical temperature is suppressed from its mean-field value and how the critical behavior near the finite-temperature phase transition evolves from the mean-field to the Heisenberg universality class. By identifying the symmetry breaking of paramagnetic diagrammatic expansions as a signature of the Néel transition, we accurately predict the Néel temperature of the three-dimensional cubic Hubbard model across all interaction strengths with low computational cost. Introducing a variational order parameter, our method can be applied to both paramagnetic and long-range ordered states, such as antiferromagnetic order. We compute magnetization and antiferromagnetic susceptibility, demonstrating minor corrections to DMFT solutions in the weak-coupling regime while revealing significant modifications to these properties in the intermediate correlation regime. From the analysis of critical exponents, we establish the emergence of Heisenberg critical behavior beyond the mean-field nature of DMFT.

Read the whole article by Yueyi Wang and Kristjan Haule in Physical Review Letters.